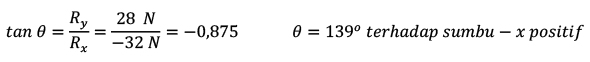Fisika / Kelas X / Vektor
Vektor adalah besaran fisika yang memiliki nilai dan arah. Contoh besaran yang termasuk vektor adalah perpindahan, kecepatan, gaya, percepatan, dan momentum. Besaran yang hanya memiliki nilai adalah besaran skalar. Contoh besaran skalar adalah jarak, massa, waktu, kuat arus, usaha, dan energi.
Vektor digambarkan dengan anak panah. Panjang anak panah merupakan besar nilai vektor tersebut dan arah anak panah menunjukkan arah vektor. Notasi vektor dituliskan dengan satu atau dua huruf dengan tanda panah di atasnya, misalnya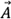 dan
dan 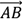 . Titik A disebut dengan titik pangkal vektor dan titik B disebut dengan ujung vektor.
. Titik A disebut dengan titik pangkal vektor dan titik B disebut dengan ujung vektor.
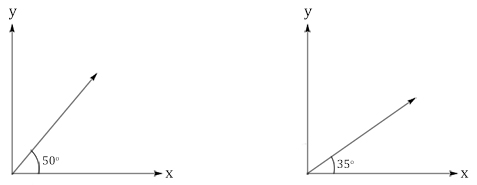
 Besar sebuah vektor dapat dituliskan dengan berbagai cara, salah satunya dituliskan dengan memberi tanda mutlak | |. Contoh, besar vektor A ditulis dengan |A| atau besar vektor B ditulis dengan |B|. Arah sebuah vektor dinyatakan dengan sudut tertentu terhadap acuan tertentu. Pada umumnya, sudut sebuah vektor dinyatakan terhadap sumbu-x positif. Contohnya seperti gambar di bawah ini.
Besar sebuah vektor dapat dituliskan dengan berbagai cara, salah satunya dituliskan dengan memberi tanda mutlak | |. Contoh, besar vektor A ditulis dengan |A| atau besar vektor B ditulis dengan |B|. Arah sebuah vektor dinyatakan dengan sudut tertentu terhadap acuan tertentu. Pada umumnya, sudut sebuah vektor dinyatakan terhadap sumbu-x positif. Contohnya seperti gambar di bawah ini.
Vektor digambarkan dengan anak panah. Panjang anak panah merupakan besar nilai vektor tersebut dan arah anak panah menunjukkan arah vektor. Notasi vektor dituliskan dengan satu atau dua huruf dengan tanda panah di atasnya, misalnya
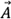 dan
dan 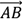 . Titik A disebut dengan titik pangkal vektor dan titik B disebut dengan ujung vektor.
. Titik A disebut dengan titik pangkal vektor dan titik B disebut dengan ujung vektor.

Penjumlahan vektor tidak sama dengan penjumlahan skalar karena vektor selain memiliki nilai juga memiliki arah. Vektor yang diperoleh dari penjumlahan beberapa vektor disebut dengan vektor resultan.
1. Resultan dua vektor sejajar
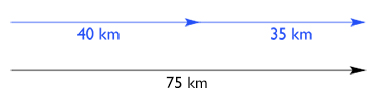
Contohnya kita pergi ke timur sejauh 40 km lalu berhenti sejenak. Kemudian perjalanan selanjutnya adalah 35 km ke arah timur lagi. Maka resultan perpindahan kita adalah 40 km + 35 km = 75 km. Secara grafis perpindahan ini digambarkan sebagai berikut.
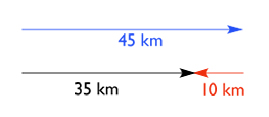
Kasus kedua, setelah kita bergerak ke arah timur sejauh 45 km, kita perlu kembali lagi ke arah barat sejauh 10 km. Maka relatif dari tempat awal perpindahan kita adalah 45 km - 10 km = 35 km. Secara grafis perpindahan ini digambarkan sebagai berikut.
Dari kedua contoh ini, jika dirumuskan secara matematis besar resultan vektor R saat vektor A dan B searah adalah:
Jika vektor A dan B berlawan arah, maka besar vektor R adalah:
2. Resultan dua vektor saling tegak lurus
Contohnya, kita pergi ke arah timur sejauh 60 km lalu ke arah utara sejauh 80 km. Secara grafis vektor ini digambarkan sebagai berikut:
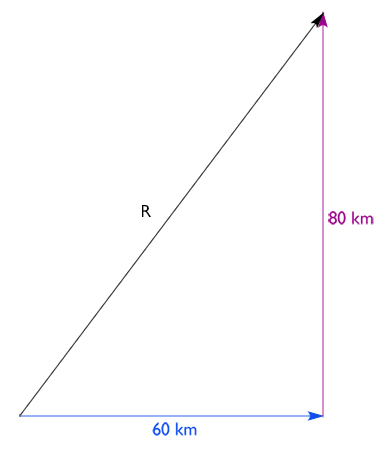 Maka untuk menghitung besar resultan r bisa menggunakan rumus Pythagoras:
Maka untuk menghitung besar resultan r bisa menggunakan rumus Pythagoras:
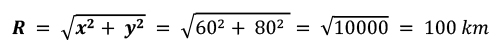 dan untuk arahnya kita menggunakan rumus tangen:
dan untuk arahnya kita menggunakan rumus tangen:
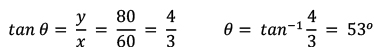 Kesimpulannya untuk dua vektor A dan B yang saling tegak lurus, vektor resultan R bisa dihitung dengan rumus:
Kesimpulannya untuk dua vektor A dan B yang saling tegak lurus, vektor resultan R bisa dihitung dengan rumus:
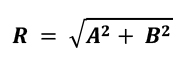 dengan arah:
dengan arah:
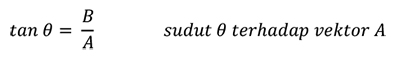
3. Resultan dua vektor yang mengapit sudut
Vektor A dan B mengapit sebuah sudut seperti ditunjukkan pada gambar kiri di bawah ini. Maka untuk mendapatkan vektor resultan R bisa digambarkan dengan menggambar pangkal vektor B pada ujung vektor A sehingga didapatkan gambar kanan di bawah ini.
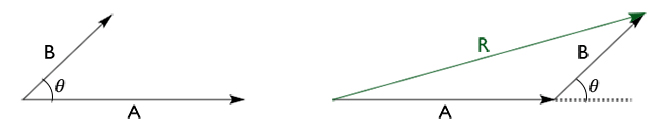 Untuk menghitung vektor R kita bisa memakai bantuan dari vektor bayangan C dan D.
Untuk menghitung vektor R kita bisa memakai bantuan dari vektor bayangan C dan D.
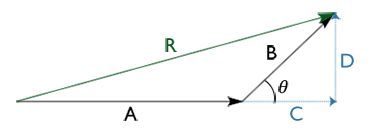 Dengan dalil Pythagoras kita mendapatkan:
Dengan dalil Pythagoras kita mendapatkan:
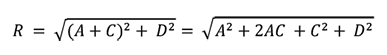 Selanjutnya dengan dalil pythagoras pada segitiga kecil BCD kita dapatkan:
Selanjutnya dengan dalil pythagoras pada segitiga kecil BCD kita dapatkan:
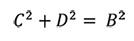 Dari trigonometri kita bisa mengetahui bahwa:
Dari trigonometri kita bisa mengetahui bahwa:
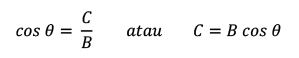 Sehingga resultan vektor R menjadi:
Sehingga resultan vektor R menjadi:
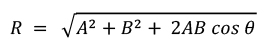
4. Selisih dua vektor yang mengapit sudut
Vektor -B adalah vektor yang memiliki besar yang sama dengan Vektor B tapi arahnya berlawanan 180o. Jadi jika digambar vektor A-B menjadi seperti ini:
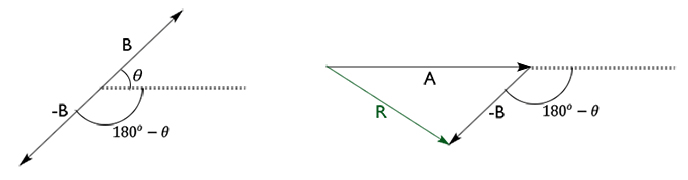 Selisih vektor dengan resultan R dituliskan R = |A-B|. Secara analisis rumus yang digunakan sama seperti sebelumnya, tetapi sudut θ menjadi 180-θ. Dalam trigonometri cos (180-θ) = -cos (θ). Sehingga persamaannya menjadi:
Selisih vektor dengan resultan R dituliskan R = |A-B|. Secara analisis rumus yang digunakan sama seperti sebelumnya, tetapi sudut θ menjadi 180-θ. Dalam trigonometri cos (180-θ) = -cos (θ). Sehingga persamaannya menjadi:
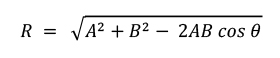
5. Menggambar vektor dengan metode poligon
Untuk menggambar beberapa vektor yang ingin dijumlahkan kita hanya perlu menggambar satu per satu vektor dengan menyambungkan titik ujung vektor pertama ke titik pangkal vektor yang berikutnya. Vektor resultannya adalah vektor dengan titik pangkal yang sama dengan vektor yang pertama dan titik ujungnya berhimpit dengan vektor yang terakhir.
Contohnya untuk vektor A, B, C di bawah ini dan gambar resultannya.
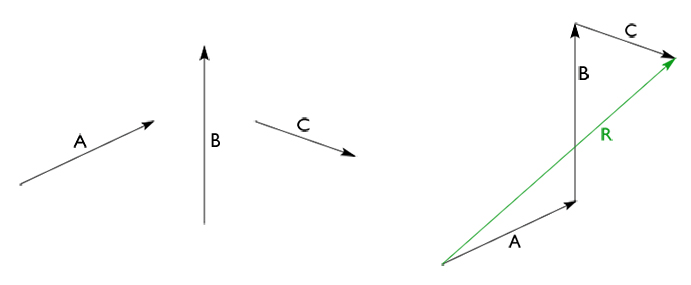 Secara matematis dituliskan dengan R = A + B + C
Secara matematis dituliskan dengan R = A + B + C
Jika vektor yang dijumlahkan pada vektor akhirnya bertemu dengan titik pangkal vektor yang pertama maka disebut dengan vektor nol. Contohnya vektor berikut ini:
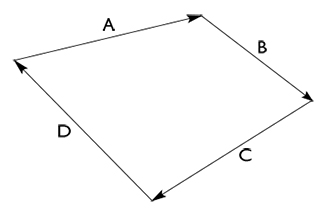 maka secara matematis R = A + B + C + D = 0
maka secara matematis R = A + B + C + D = 0
1. Resultan dua vektor sejajar
Contohnya kita pergi ke timur sejauh 40 km lalu berhenti sejenak. Kemudian perjalanan selanjutnya adalah 35 km ke arah timur lagi. Maka resultan perpindahan kita adalah 40 km + 35 km = 75 km. Secara grafis perpindahan ini digambarkan sebagai berikut.

Kasus kedua, setelah kita bergerak ke arah timur sejauh 45 km, kita perlu kembali lagi ke arah barat sejauh 10 km. Maka relatif dari tempat awal perpindahan kita adalah 45 km - 10 km = 35 km. Secara grafis perpindahan ini digambarkan sebagai berikut.

Dari kedua contoh ini, jika dirumuskan secara matematis besar resultan vektor R saat vektor A dan B searah adalah:
R = |A+B| dengan arah R searah dengan arah vektor A dan B
R = |A-B| dengan arah R searah dengan arah vektor terbesar
2. Resultan dua vektor saling tegak lurus
Contohnya, kita pergi ke arah timur sejauh 60 km lalu ke arah utara sejauh 80 km. Secara grafis vektor ini digambarkan sebagai berikut:

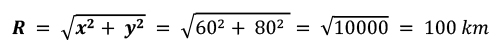
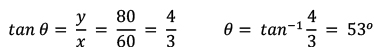
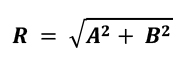
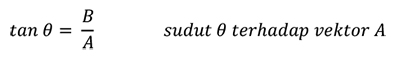
3. Resultan dua vektor yang mengapit sudut
Vektor A dan B mengapit sebuah sudut seperti ditunjukkan pada gambar kiri di bawah ini. Maka untuk mendapatkan vektor resultan R bisa digambarkan dengan menggambar pangkal vektor B pada ujung vektor A sehingga didapatkan gambar kanan di bawah ini.


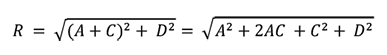
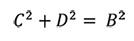
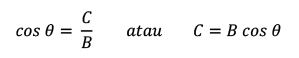
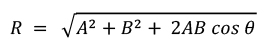
4. Selisih dua vektor yang mengapit sudut
Vektor -B adalah vektor yang memiliki besar yang sama dengan Vektor B tapi arahnya berlawanan 180o. Jadi jika digambar vektor A-B menjadi seperti ini:

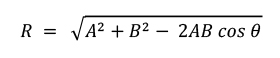
5. Menggambar vektor dengan metode poligon
Untuk menggambar beberapa vektor yang ingin dijumlahkan kita hanya perlu menggambar satu per satu vektor dengan menyambungkan titik ujung vektor pertama ke titik pangkal vektor yang berikutnya. Vektor resultannya adalah vektor dengan titik pangkal yang sama dengan vektor yang pertama dan titik ujungnya berhimpit dengan vektor yang terakhir.
Contohnya untuk vektor A, B, C di bawah ini dan gambar resultannya.

Jika vektor yang dijumlahkan pada vektor akhirnya bertemu dengan titik pangkal vektor yang pertama maka disebut dengan vektor nol. Contohnya vektor berikut ini:

Secara grafis, beberapa vektor dijumlah dengan metode poligon yang sudah dibahas sebelumnya. Bagaimana cara menghitung besar dan arah resultannya? Di sinilah kita membutuhkan metode uraian.
Menguraikan vektor menjadi komponennya
Sebuah vektor dapat diuraikan menjadi dua vektor yang tegak lurus: vektor terhadap sumbu-x dan sumbu-y. Contohnya pada gambar ini ada vektor A dan vektor komponnenya: vektor Ax dan vektor Ay.
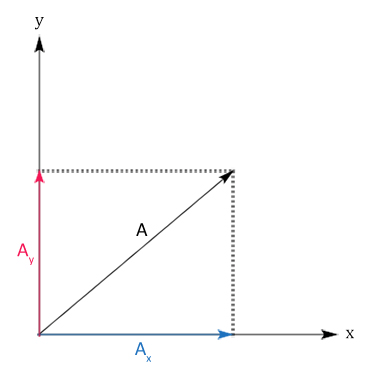 Berdasarkan trigonometri kita bisa menghitung vektor x dan vektor y dengan menggunakan hubungan antara sudut dan panjang vektor A tersebut. Maka besar vektor komponen adalah sebagai berikut:
Berdasarkan trigonometri kita bisa menghitung vektor x dan vektor y dengan menggunakan hubungan antara sudut dan panjang vektor A tersebut. Maka besar vektor komponen adalah sebagai berikut:
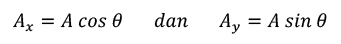
Menjumlahkan vektor melalui komponen-komponennya
Jika terdapat banyak vektor yang ingin dijumlahkan, kita bisa menggunakan tahap-tahap berikut:
1. Semua vektor yang ingin dijumlahkan masing-masing diuraikan ke dalam sumbu-x dan sumbu-y.
2. Jumlahkan semua vektor yang berada pada sumbu masing-masing sehingga jumlah vektor pada sumbu-x menjadi Rx dan pada sumbu-y menjadi Ry.
3. Untuk menentukan resultan semuanya maka digunakan dalil pythaghoras:
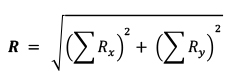 4. Arah vektor resultannya bisa dihitung dengan menggunakan trigonometri:
4. Arah vektor resultannya bisa dihitung dengan menggunakan trigonometri:
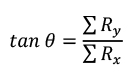
Contoh soalnya adalah sebagai berikut. Terdapat 3 vektor gaya dengan besar dan arah masing-masing: F1 = 20 N arah 37o terhadap sumbu-x positif, F2 = 50 N arah 127o terhadap sumbu-x positif, dan F3 = 30 N arah 233o terhadap sumbu-x positif. Sehingga digambarkan sebagai berikut:
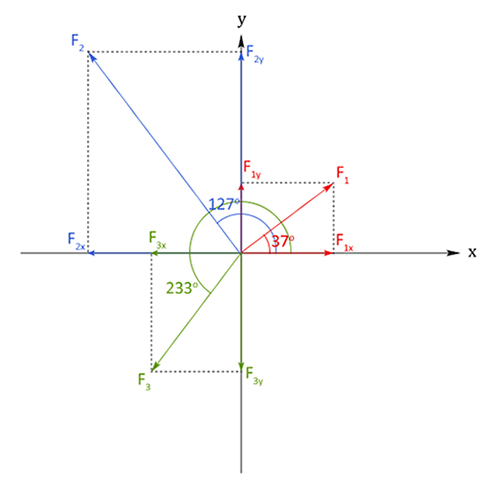 Maka besar tiap uraian:
Maka besar tiap uraian:
F1x = F1 cos 37o = 20 N x 0,8 = 16 N
F1y = F1 sin 37o = 20 N x 0,6 = 12 N
F2x = F2 cos 127o = 50 N x -0,6 = -30 N
F2y = F2 sin 127o = 50 N x 0,8 = 40 N
F3x = F3 cos 233o = 30 N x -0,6 = -18 N
F3y = F3 sin 233o = 30 N x -0,8 = -24 N
Resultan vektornya:
Rx = 16 -30 - 18 = -32 N
Ry = 12 + 40 - 24 = 28 N
Arahnya:
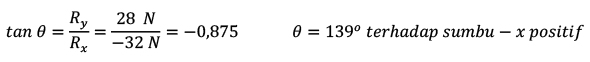
Menguraikan vektor menjadi komponennya
Sebuah vektor dapat diuraikan menjadi dua vektor yang tegak lurus: vektor terhadap sumbu-x dan sumbu-y. Contohnya pada gambar ini ada vektor A dan vektor komponnenya: vektor Ax dan vektor Ay.

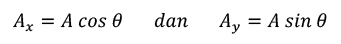
Menjumlahkan vektor melalui komponen-komponennya
Jika terdapat banyak vektor yang ingin dijumlahkan, kita bisa menggunakan tahap-tahap berikut:
1. Semua vektor yang ingin dijumlahkan masing-masing diuraikan ke dalam sumbu-x dan sumbu-y.
2. Jumlahkan semua vektor yang berada pada sumbu masing-masing sehingga jumlah vektor pada sumbu-x menjadi Rx dan pada sumbu-y menjadi Ry.
3. Untuk menentukan resultan semuanya maka digunakan dalil pythaghoras:
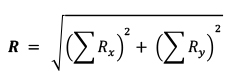
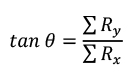
Contoh soalnya adalah sebagai berikut. Terdapat 3 vektor gaya dengan besar dan arah masing-masing: F1 = 20 N arah 37o terhadap sumbu-x positif, F2 = 50 N arah 127o terhadap sumbu-x positif, dan F3 = 30 N arah 233o terhadap sumbu-x positif. Sehingga digambarkan sebagai berikut:

F1x = F1 cos 37o = 20 N x 0,8 = 16 N
F1y = F1 sin 37o = 20 N x 0,6 = 12 N
F2x = F2 cos 127o = 50 N x -0,6 = -30 N
F2y = F2 sin 127o = 50 N x 0,8 = 40 N
F3x = F3 cos 233o = 30 N x -0,6 = -18 N
F3y = F3 sin 233o = 30 N x -0,8 = -24 N
Resultan vektornya:
Rx = 16 -30 - 18 = -32 N
Ry = 12 + 40 - 24 = 28 N
Arahnya: